Räkna med Delphi
Förord
När det gäller tal, beräkningar och datatyper så erbjuder Delphi många sofistikerade metoder. Det finns också många fallgropar för den ovane att fall ned i, särskilt när det gäller datatyper och konvertering av dessa. Denna artikel skall förhoppningsvis klargöra de grundläggande metoderna för hur du hanterar tal och hur du räknar med hjälp av relaterade datatyper i Delphi.Innehåll
»»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
Enkla datatyper
I Object Pascal finns en mängd olika datatyper att välja bland för en variabel, beroende på vad för slags data som skall lagras i variabeln och dels på vilket sätt man skall använda data på.I detta kapitel skall vi beröra datatyper för heltal och s k flyttal. Dessa hör till de enkla datatyperna till skillnad från string som är en sammansatt datatyp.
Till de enkla datatyperna räknas alla heltalstyper och flyttalstyper samt dessutom datatyperna char och boolean som behandlas senare.
Heltalstyper
Det som karakteriseras av en datatyp för heltal är naturligtvis att alla värden i talområdet är hela tal. Men det innebär också att alla värden i datatypen går att räkna upp, det finns endast ett ändligt antal. Ett givet tal i talområdet kan alltid representeras av exakt av en heltalsvariabel. Beroende på storleken av talområdet krävs olika många minnesceller, byte, till de olika heltalstyperna. En minnescell i datorn svarar mot en byte, som i sin tur kan innehålla 8 bitar. En bit kan bara innehålla ett binärt värde, 0 eller 1.I tabellen nedan presenteras de datatyper för heltal som finns i Object Pascal. Datatyp
| Datatyp | Talområde | Byte |
|---|---|---|
| shortint | -128..127 | 1 |
| smallint | -32768..32767 | 2 |
| integer, longint | -2147483648..2147483647 | 4 |
| byte | 0..255 | 1 |
| word | 0..65535 | 2 |
| cardinal | 0..2147483547 | 4 |
Flyttalstyper
Utmärkande för flyttalstyperna är att de skall kunna representera tal med ett flytande decimaltecken, dvs decimala tal.Notera följande!
- Flyttal skrivs alltid med en decimalpunkt, aldrig ett decimalkomma.
- En flyttalstyp kan innehålla oändligt många värden även om talområdet är begränsat.
- Ett flyttal kan vara exakt lika stort som ett givet tal. Oftast är flyttalet endast ungefär lika stort som det givna talet. Detta hänger ihop med att flyttalet skall representera det givna talet med hjälp av ett begränsat antal minesceller.
I tabellen nedan menas med skrivsättet +-2.9*10-39 .. +-1.7*1038 både talområdet -1.71038 och talområdet 2.9*10-39.. 1.7*1038. Den näst sista datatypen i tabellen är inget flyttal. Comp är en datatyp som utnyttjar matematikprocessorn och kan enbart representera tal.
Tabell med datatyper för flyttal.
| Datatyp | Talområde | Signifikanta siffror | Byte |
|---|---|---|---|
| real | +-2.9*10-39 .. +-1.7*1038 | 11 - 12 | 6 |
| single | +-1.5*10-45 .. +-3.4*1038 | 7 - 8 | 4 |
| double | +-5.0*10-324 .. +-1.7*10308 | 15 - 16 | 8 |
| extended | +-1.9*10-4932 .. +-1.1*104932 | 19 - 20 | 10 |
| comp | -263 .. 263 -1 | 19 - 20 | 8 |
| currency | -922337203685477.5808 .. 922337203685477.5807 | 19 - 20 | 8 |
Heltal contra flyttal
Heltalstyper
- kan representera talvärden exakt
- tar liten plats
- går snabbt att räkna med
Flyttalstyper (t ex double)
- kan representera stora tal
- men endast ungefär
- tar stor plats
- tar längre tid att räkna med
Allmänt gäller
- Kan du klara dig med heltal så väljer du en heltalstyp. En heltalstyp tar mindre plats och representerar ett exakt värde som går snabbare att göra beräkningar med.
- Flyttal används vid mycket stora tal och vid decimala tal.
Deklaration och tilldelning av talvariabler
Talvariabler deklareras på samma sätt som strängvariabler. Namnen på variablerna väljer du efter de namngivningsregler som vi har diskuterat tidigare.
var
x, y, faktor : double;
i,j,k : integer;
a,b : word;
I variabeldeklarationen räknas upp ett antal variabler. För varje variabel anges en datatyp, så att till variabeln kan reserveras det minne som krävs. Variabler av olika datatyp går bra att räkna upp i samma variabeldeklaration.
Några exempel av variabeltilldelningar.
x := 1e-12; {double}
y := 2.718; {double}
k := 2.718; {integer}
a := 2000000000; {word}
Konvertering mellan talsträng och talvärde
Eftersom utskrifter alltid sker med hjälp av strängar, t ex med hjälp av Caption för en Label, måste man kunna översätta talvärden till strängar. Inmatning av ett värde görs i Delphi oftast med hjälp av egenskapen Text hos editeringsrutan, dvs inmatningen görs till en talsträng som som du inte kan utföra räkneoperationer med. Här måste det då göras en översättning från en talsträng till motsvarande talvärde. Översättningar (konverteringar) från talsträngar till talvärde eller tvärtom är därför en viktig detalj i Delphi.Några konverteringsexempel. Först görs några variabeldeklarationer:
var
a : integer;
x : double;
s : string;
...sedan följer således några konverteringsexempel:
a =: StrToInt('123'); {Strängen '123' översätts till talvärdet 123 och lagras i variabeln a}
x = : StrToFloat('123,456'); {Strängen '123,456' översätts till talvärdet 123.456 och lagras i variabeln x}
s = : IntToStr(123); {Talet 123 översätts till strängen '123' och lagras i variabeln s}
s = : FloatToStr(123.456); {Talet 123.456 översätts till strängen '123,456' och lagras i variabeln s}
Vid konverteringen från sträng till flyttal och tvärtom med dessa rutiner används den representation av decimaltecknet som gäller för Windows. I de här fallen måste alltså decimaltecknet i strängarna skrivas som ett decimalkomma. Och när Delphi översätter från ett talvärde till en talsträng skriver Delphi decimaltecknet som ett decimalkomma.
Andra konverteringsrutiner
Med konverteringsrutinerna ovan klara du av de flesta situationer. När man vill översätta ett flyttal till en sträng vill man emellertid ofta ha möjlighet att formatera textsträngen. Man kanske vill ha ett visst antal decimaler, eller kanske ha talet på decimalform eller på exponentform etc.En konverteringsrutin som klarar detta är FloatToStrF.
I föregående exempel användes instruktionen
Label.Caption := FloatToStr(x);
Om vi istället vill använda FloatToStrF och vill att resultatet skall bli ett decimalt tal med två decimaler och 4 gällande siffror så skriver vi:
Label.Caption := FloatToStrF(x,ffFixed,4,2);
Allmänt skriver man
Label.Caption := FloatToStrF(x,format,precision,digits);
där format är formateringssättet, precision är antalet gällande siffror och digits antingen står för antalet decimaler eller antalet siffror i exponenten. I tabellen nedan beskrivs de olika formateringssätten.
| Formateringssätt | Innebörd |
|---|---|
| ffFixed | Decimalformat. Talet konverteras till en sträng på formatet "-ddd.dd". Strängen inleds med ett minustecken om talet är negativt och minst en siffra föregår alltid decimaltecknet. Den angivna precisionen anger hur många siffror som skall vara gällande. Om precisionen är mindre än antalet siffror före decimaltecknet skrivs talet på exponentform. Antalet decimaler anges med digits i intervallet 0..18. |
| ffExponent | Exponentformat. Talet skrivs på formen " -d.ddd...E+dddd". Strängen inleds med ett minustecken om talet är negativt och precis en siffra föregår decimaltecknet. Den angivna precisionen anger hur många värdesiffror som strängen skall innehålla. |
| ffGeneral | Allmänt format. Talvärdet Talvärdet konverteras till kortast möjliga talsträng på decimal- eller exponentformat. Decimaltecknet visas enbart om det behövs. |
| ffNumber | Decimalformat. Samma som ffFixed med tillägget att talsträngen förses med avgränsare för tusental. |
| ffCurrency | Myntformat. Samma som ffNumber med myntslaget angivet efter strängen, dvs "kr". |
Kompabilitet mellan heltalstyper
Här följer en procedur som demonstrerar kompabiliteten mellan olika datatyper.
procedure TForm1.Button1Click(Sender: TObject);
var
a : byte;
b : word;
c : integer;
x : double;
begin
x := 8; {Tilldelning med konstantvärde}
c := 7; {Tilldelning mellan variabler av olika heltalstyp går bra så länge
a := c; värdet ryms inom typerna}
b := c;
Label1.Caption := IntToStr(a);
Label2.Caption := IntToStr(b);
Label3.Caption := IntToStr(c);
Label4.Caption := FloatToStr(x);
end;
Konverteringarna mellan heltalstyperna i proceduren ovan möter inga problem så länge värdena håller sig inom ramen för vad datatyperna tillåter och de kan därmed sägas vara kompatibla.
Följande sats däremot protesterar kompilatorn emot.
a := x; {OBS! fungerar ej!}
Vi försöker här tilldela en bytevariabel värdet av en flyttalsvariabel. En bytevariabel tar upp en byte av minnet medan en flyttalsvariabel av typen double kräver 8 minnesceller. Av det skälet fungerar inte denna tilldelning. Däremot går det omvända alldeles utmärkt:
x := a; {Fungerar!!!}
Beräkningsuttryck
Naturligtvis går det bra att använda variabler i beräkningsuttryck. För att demonstrera detta skall vi göra ett litet ränteexempel.Placera ut två editeringsrutor på ett formulär. Förse dem med etiketter med ledtexter enligt bilden. Sätt Caption för Label3 till en tom sträng.
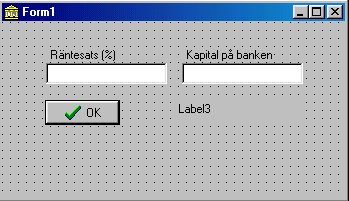
Dubbelklicka sedan på knappen och komplettera händelseproceduren enligt nedan.
procedure TForm1.BitBtn1Click(Sender: TObject);
var
proc, kap, nykap : double;
begin
proc := StrToFloat(Edit1.Text);
kap := StrToFloat(Edit2.Text);
nykap := kap*(1+proc/100);
Label3.Caption := 'På ett år växer detta till ' + FloatToStrF(nykap, ffCurrency,10,2);
end;
Provkör sedan programmet.
I proceduren tilldelas variablerna sina värden från editeringsrutorna. Därefter utförs ränteberäkningen och läggs i variabeln nykap. Värdet i nykap konverteras till en textsträng med hjälp av FloatToStrF till myntformat (kr). Slutligen skrivs resultatet ut i Label3.
Spin och Gauge
Vi skall nu se hur variabler kan användas i ett program, där vi samtidigt passar på att bekanta oss med komponenterna Spin och Gauge. Du hittar dessa på fliken Samples i komponentpaletten.Gauge-komponenten är en slags visare som kan visa värden i intervallet 0..100%. Spin-komponenten är avsedd för upp- eller nedräkning.
Placera ut en Spin- och en Gauge-komponent på ett formulär. Lägg även till en etikett och en editeringsruta enligt bilden nedan. Ändra editeringsrutans ReadOnly-egenskap till True.
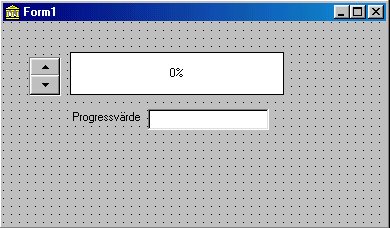
Ändra sedan Gaugekomponentens egenskap MinValue till 10 och MaxValue till 30. Sätt egenskapen Kind till gkPie (cirkel). Välj sedan Spinkomponenten i Objektinspektorn och klicka på fliken Events. Komplettera därefter händelsen OnDownClick enligt nedan.
procedure TForm1.SpinButton1DownClick(Sender: TObject);
var a : integer;
begin
a := Gauge1.Progress - 1;
Gauge1.Progress:= a;
Edit1.Text := IntToStr(Gauge1.Progress);
end;
Klicka i värderutan för händelsen OnUpClick och komplettera proceduren.
procedure TForm1.SpinButton1UpClick(Sender: TObject);
var a : integer;
begin
a := Gauge1.Progress + 1;
Gauge1.Progress:= a;
Edit1.Text := IntToStr(Gauge1.Progress);
end;
Kör sedan programmet!
Som du ser ändras värdet på Gauge-komponenten med 5% i taget.
Ord, Pred och Succ
På alla skalära datatyper kan du använda ordningsfunktionerna Ord, Pred och Succ. Här skall vi visa ett exempel på hur dessa används.Placera en editeringsruta försedd med texten "Testvärde". Koppla en UpDown-komponent till editeringsrutan. Ändra Position för UpDown-komponenten till 50 i Objektinspektorn. Placera ytterligare tre etiketter under editeringsrutan och en knapp med texten "Visa ordningstal". Klicka på knappen och skriv följande procedur.
procedure TForm1.Button1Click(Sender: TObject);
var a,y,z : smallint;
begin
x := UpDown1.Position;
y := Pred(x);
z := Succ(x);
Label2.Caption := 'Talet '+Edit1.Text+ 'har ordningsnumret '+IntToStr(Ord(x));
Label3.Caption := 'Föregående tal är '+IntToStr(y);
Label4.Caption := 'Efterföljande tal är '+IntToStr(z);
end;
Ord(x) ger alltså ordningsnumret på det värde som x innehåller.
Pred(x) och Succ(x) ger föregående resp efterföljande värde till x.
Att som ovan använda Ord på heltalstyper är självfallet meningslöst men kan vara till nytta på typerna char och boolean.
Däremot kan Pred och Succ vara användbara på heltal.
Pred(x) ger värdet x-1
Succ(x) ger värdet x+1
Funktionerna Ord, Pred och Succ kan inte användas på flyttalstyper.
Low och High
Dessa två funktion används för att ta reda på det minsta resp det största värdet i en viss datatyp.Ett exempel:
procedure TForm1.Button1Click(Sender: TObject);
begin
Edit1.Text := IntToStr(Low(shortint));
Edit2.Text := IntToStr(Low(smallint));
end;
Inc och Dec
Två andra mycket snabba funktioner är Inc och Dec som är avsedda att räkna upp eller ned värden av heltalstyper.Inc(x) är detsamma som x := x + 1;
Dec(x) är detsamma som x := x - 1;
Vill man ändra värdet med mer än ett steg, anger man ett värde för detta avgränsat med kommatecken.
Inc(x,3) är detsamma som x := x + 3;
Dec(x,5) är detsamma som x := x - 5;
Div och Mod
Två användbara heltalsoperatorer är div och mod.Exempel på dessa.
41 div 7 = 5
Anger hur många hela gånger som 7 går i 41.
41 mod 7 = 6
Utgör den rest som blir över vid divisionen, dvs. 41-7*5
Trunc(x) och Round(x)
- Trunc(x) ger det trunkerade, "avklippta", heltalsvärdet av flyttalet x.
- Round(x) ger det avrundade heltalsvärdet av x.
Exempel på funktionerna Trunc(x) och Round(x).
Trunc(8.4) ger heltalsvärdet 8.
Trunc(8.7) ger heltalsvärdet 8.
Trunc(-9.2) ger heltalsvärdet -9.
Trunc(-8.7) ger heltalsvärdet -8.
Round(8.4) ger heltalsvärdet 8.
Round(8.5) ger heltalsvärdet 9.
Round(-9.4) ger heltalsvärdet -9.
Round(-9.5) ger heltalsvärdet -10.
Int och Frac
- Int(x) trunkerar ett flyttal och resultatet blir av flyttalstyp.
- Frac(x) ger decimaldelen av ett flyttal.
Exempel på funktionerna Int(x) och Frac(x).
Int(8.7) ger flyttalsvärdet 8.0000
Frac(8.7) ger flyttalsvärdet 0.70000
Int(-9.2) ger flyttalsvärdet -9.0000
Frac(-9.2) ger flyttalsvärdet -0.20000
Slumptal
Funktioner som skapar slumptal är Random och Random(n). - Random ger slumptal av flyttalstyp från 0 upp till 1.
- Random(n) ger slumptal i form av heltal från 0 och upp t o m n-1.
Anta att x är en flyttalsvariabel och a är en heltalsvariabel.
x := Random; {Ger slumptal 0.0000 <=x< 1.0000}
x := 100*Random; {Ger slumptal 0.0000 <=x< 100.0000}
x := 5+10*Random; {Ger slumptal 5.0000 <=x< 15.0000}
a := Random(10); {Ger slumptal 0 <=a< 10-1}
a := Random(6); {Ger slumptal 0 <=a<= 5}
a := 1+Random(6); {Ger slumptal 1 <=a<= 6}
a := -5+Random(11); {Ger slumptal -5 <=a<= 5}
I Object Pascal genereras alltid slumptalen på ett visst sätt. Vill man ha en följd av slumptal anropar man Random-funktionen för så många tal man vill ha. Problemet är bara att det alltid är samma slumptalsföljd man får.
För att komma bort från denna olägenhet kan man använda proceduren Randomize. Med Randomize garanteras att slumptalföljden alltid startar med ett slumpvis startvärde. Man får då verkligen en slumpmässig följd.
Det räcker med att anropa Randomize en enda gång i händelseproceduren.
0 Kommentarer